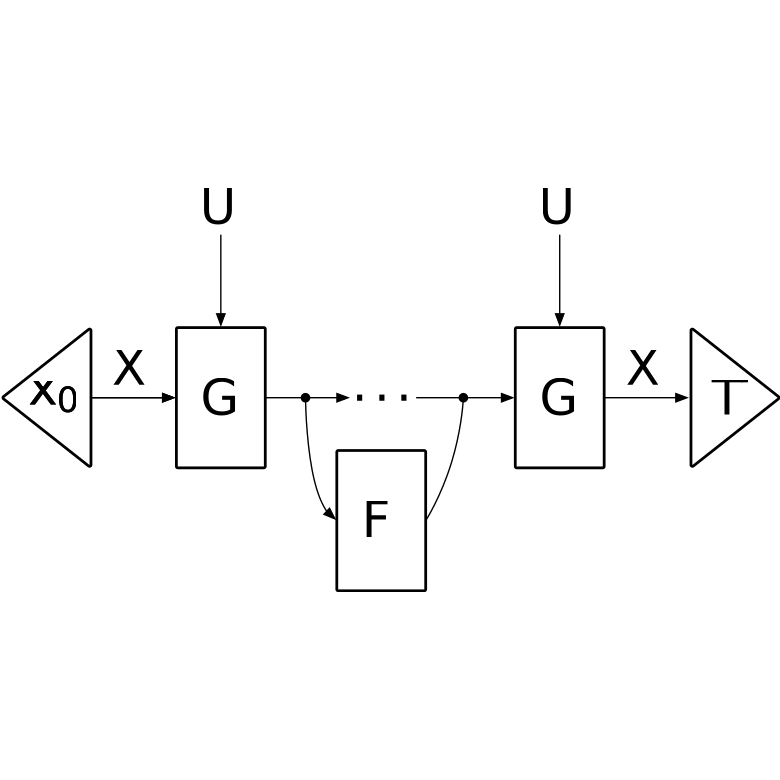
Model predictive control (MPC) is an optimal control technique which involves solving a sequence of constrained optimization problems across a given time horizon. We present a novel Julia library that leverages our theoretical results to automate the implementation of correct-by-construction MPC problems in software.
Project Team
| Name | Member Since | Degree | Program | |
|---|---|---|---|---|

|
Tyler Hanks | 2021 | PhD | CISE |

|
Samuel Cohen | |||

|
Richard Samuelson | 2024 |
No matching items
Project Articles
-
Modeling Model Predictive Control: A Category Theoretic Framework for Multistage Control Problems
American Control Conference (2024)
Details DOI URL Preprint -
Generalized Gradient Descent is a Hypergraph Functor
Applied Category Theory (2024)
Details -
A Compositional Framework for First-Order Optimization
arxiv (2024)
Details DOI URL Preprint -
Characterizing Compositionality of LQR from the Categorical Perspective
IEEE Conf. Decision and Control (2023)
Details DOI URL Preprint -
Typed and stratified models with slice categories
Applied Category Theory 2022 (2022)
Details -
An Algebraic Framework for Structured Epidemic Modeling
Proc. of the Royal Society Phil. Trans. (2022)
Details DOI URL -
Operadic Modeling of Dynamical Systems: Mathematics and Computation
Applied category Theory (Proceedings) (2021)
Details URL -
AlgebraicDynamics: Compositional dynamical systems
JuliaCon, Online (2021)
Details URL
No matching items
Sponsors
AlgebraicOptimization and Control has been supported by the following programs:
- NSF: Graduate Research Fellowship Program
- ONR: Domain Transfer for Continuity of Performance
- AFRL: Griffis Summer Internship Program